반응형
함수
- 함수 f는 A의 원소 각각에 B의 원소를 단 하나만 대응시킨 것이다.
- 정의역 : A의 모든 원소
- 공역 : B의 모든 원소
- 치역 : 정의역의 각 원소에 실제로 대응되는 값만 모아놓은 B의 부분집합 (공역의 부분집합)
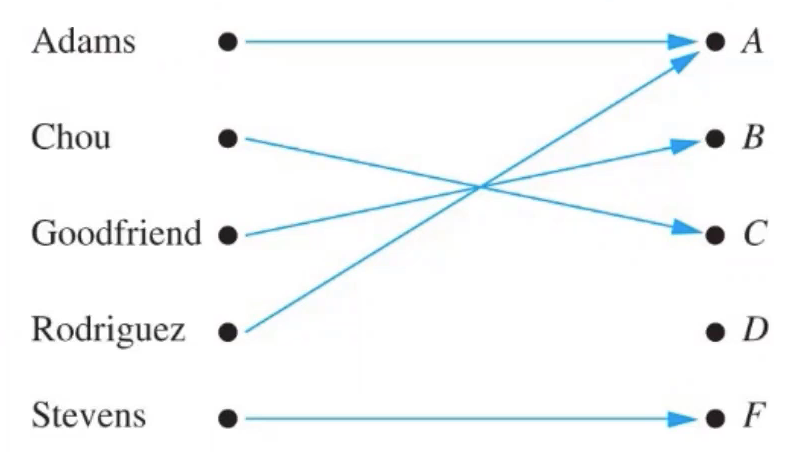
#함수의 예시
f가 A로부터 B로의 함수일 때 f : A -> B
라고 쓴다.
다음은 공역, 치역의 개념을 잘 이해할 수 있는 예제 문제이다.

함수의 연산

함수는 곱하기와 덧셈 연산이 성립한다.
단사함수 - 일대일 함수
- f의 정의역에 속한 모든 a와 b에 있어서 f(a) = f(b)이면 반드시 a = b 일 때, 함수 f를 단사함수라고 한다.
- 일대일 함수를 의미한다.
- 공역에 있는 원소가 정의역에 있는 원소에 대해 화살표를 하나만 맞을 때,
단사 함수라고 한다. - 수학적 개념을 풀어쓴 이해 ㅎㅎ

# 단사함수가 보장되는 조건
- 증가함수
- 단조 증가함수 | 무조건 증가하는 함수
- 단조 증가함수 | 무조건 증가하는 함수
- 감소함수
- 단조 감소함수 | 무조건 감소하는 함수
전사 함수
- 공역에 있는 모든 원소가 정의역에 있는 모든 원소의 화살표를 모두 매핑이 된 함수
- 정의역 A, 공역 B가 있을 때, b ∈ B인 모든 원소에 대하여 f(a) = b인 원소 a ∈ A가 존재할 경우 f를 전사 함수라고 한다.
- 치역과 공역이 같은 경우, 즉, 공역에 속하는 모든 원소가 정의역에 속하는 어떤 원소와 매핑이 되는 경우를 전사 함수라 한다

전단사 함수 - 일대일 함수
- 단사 함수이고, 동시에 전사 함수인 함수를 전단사 함수라고 한다.
- 모든 정의역의 원소가 모든 공역의 원소에 대해 매핑이 되고, 이 매핑된 건 고유할 때 전단사 함수라고 한다.

단사 함수와 전사 함수 판정

역함수
- f의 역함수는 B의 원소 b에 A의 원소 a를 다른 것과 중복되지 않게 대응시키는 함수이다.
- 즉, f(a) = b인 f의 역함수는 f^{-1}로 표기하고 f^{-1}(b) = a인 함수이다.
- 즉, f(a) = b인 f의 역함수는 f^{-1}로 표기하고 f^{-1}(b) = a인 함수이다.
- 함수 f가 전단사 함수가 아니면 역함수를 만들 수 없다.
- 함수의 의미로 보면, 단사 함수, 전사 함수의 공역이 정의역으로 바꿔서 생각해보면
단사, 전사 함수의 역함수는 함수가 아니게 되어버리기 때문이다 ㅎㅎ..
- 함수의 의미로 보면, 단사 함수, 전사 함수의 공역이 정의역으로 바꿔서 생각해보면
따라서, 역함수에 대해 정리해보자.
- 전단사 함수는 역함수를 만들 수 있으므로 가역 함수라고 한다.
- 전단사 함수가 아닌 경우 비가역 함수라고 한다.
가역함수 : 전단사 함수
비가역 함수 : 전단사 함수가 아닌 모든 함수
함수의 활용 - 함수의 합성
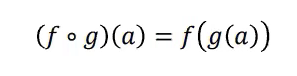
- 주의할 점은, g의 치역이 f의 정의역의 부분집합이 아니면 합성 함수 f - g는 정의할 수가 없다.
함수의 그래프
- f를 집합 A로부터 B로의 함수라고 하면 함수 f의 그래프는 {(a,b) | a ∈ A 이고 f(a) = b, b ∈ B }인 순서쌍의 집합이다.
아래 예제를 통해 그래프와 관련한 시험에 출제만을 확인하자 ㅎㅎ

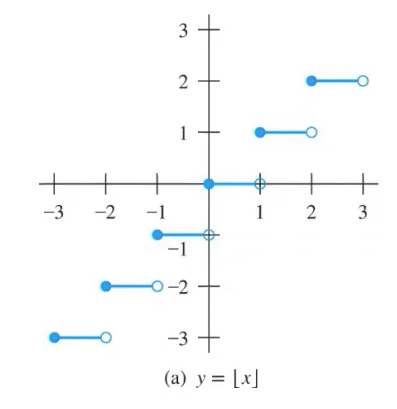
바닥 함수와 천장 함수 - 가우스 함수
- 쉽게말해서 내림과 올린 함수라고 생각하면 되겠다.
- 가우스 함수와 같다.
# 바닥함수는 가우스 기호가 밑에만 꺽여있고, 천장함수는 가우스 기호가 위에만 꺽여있다.

반응형
'CS 대학강의' 카테고리의 다른 글
| [CS 1-2 | 대학생을 위한 실용금융] 금융회사, 저축의 이해 4주차 (0) | 2022.09.28 |
|---|---|
| [CS 1-2 | 시스템 프로그래밍 기초] 함수, 메모리에서의 변수&함수 7주차 (0) | 2022.09.27 |
| [CS 1-2 | 이산수학] 집합 그리고 활용 6주차 (0) | 2022.09.26 |
| [CS 1-2 | 아카데믹 글쓰기] 고정관념, 여러 관점에서의 글쓰는 방법 3주차 (0) | 2022.09.26 |
| [CS 1-2 | 시스템 프로그래밍 기초] 피연산자와 연산자 7주차 (0) | 2022.09.23 |
