집합의 표현법 - 원소나열법
- 집합이란, 순서를 고려하지 않은 서로 다른 개체(object)들의 모임이다.
- 집합에 속한 개체는 원소 또는 구성원이라고 한다.
- 집합은 그 원소를 포함한다고 한다.

# 집합의 표현법 1.
원소 나열법
- 집합의 원소를 모두 나열하는 것
- 중괄호 '{ }' 안에 원소를 모두 나열
예를 들어 집합 A의 원소가 a, b, c, d라면 A = {a, b, c, d}로 나타낸다.

# 집합의 표현법 2.
조건 제시법
- 집합의 원소들의 공통적인 특성을 기술하는 것
- 모든 원소를 나열하는 것이 불가능한 경우 주로 사용한다.
- {x | x는 속성 P를 갖고 있다.} 는 속성 P를 갖는 모든 x들의 집합이라 읽는다.
예를 들어 10보다 작은 양의 홀수 정수의 집합 O는 O = {x | x는 10보다 작은 양의 홀수 정수}로 나타낸다.
- 조건 제시법에 사용하는 대표적인 기호

부분집합

진부분집합
- A가 B의 부분집합이지만 A != B인 것을 확실히 하고 싶을 때 진부분집합을 이용


부분집합의 활용 - 같음의 표현
- 두 개의 집합이 서로에 대해 부분집합이라면, 그 두 집합은 같은 집합이 된다.

집합의 크기
- S를 집합이라 하고, n은 음수가 아닌 정수라 하자.
S에 n개의 서로 다른 원소가 존재하면 S는 유한집합이고, n은 집합 S의 크기이다.
집합 S의 크기는 |S|로 표기한다.
멱집합
- 임의의 집합 S가 주어졌을 때 집합 S의 멱집합은 집합 S의 모든 부분집합의 집합이다.
S의 멱집합은 P(S)로 표기한다.
- 만약 집합이 n개의 원소를 가지면 그 멱집합은 2^n 개의 원소를 갖는다.

데카르트 곱
- 집합은 원소의 순서를 무시하지만, 데카르트 곱은 순서를 고려한다고 가정한다.
- 순서가 있는 n짝이라고 한다.

- 두 순서가 있는 n짝은 대응되는 원소들이 일치할 경우 서로 같다고 한다.
- a(i) = b(i), i = 1, 2, 3, ... , n일 때 (a1, a2, ... , an) = (b1, b2, ... , bn)
- 두 순서쌍 (a, b)와 (c, d)는 a = c, b = d 일 때 서로 같다고 한다.


데카르트 곱 확장


관계
- 데카르트 곱 A X B의 부분집합 R을 집합 A로부터 집합 B로의 관계라고 한다.


한정기호와 집합 표기의 사용
- 특수한 표기법을 이용하여 수학적 명제의 정의역을 표현하는 경우가 있다.


진리 집합
- 술어 P와 정의역 D가 주어졌을 때 P(x)를 참으로 만드는 원소들의 집합이다.
- P(x)의 진리집합은 {x =>> D | P(x)}로 표기한다.

- 정의역 U가 주어졌을 때 [전칭모든기호]P(x)는 P의 진리 집합이 정의역 U와 같을 때 참이다.
- 마찬가지로 존재어떤기호P(x)는 P의 진리 집합이 공집합이 아닐 때 참이다.
합집합과 교집합


차집합과 대칭차집합


여집합



집합의 대수법칙


# 대수 법칙의 증명

이 사실을 증명하기 위해선,
앞의 명제가 뒤의 명제로 된다와
뒤의 명제가 앞의 명제가 된다라는 사실을 보여주면 증명이 된다.
예제 풀이

# 조건 제시법과 논리적 동치를 이용한 증명

예제 풀이

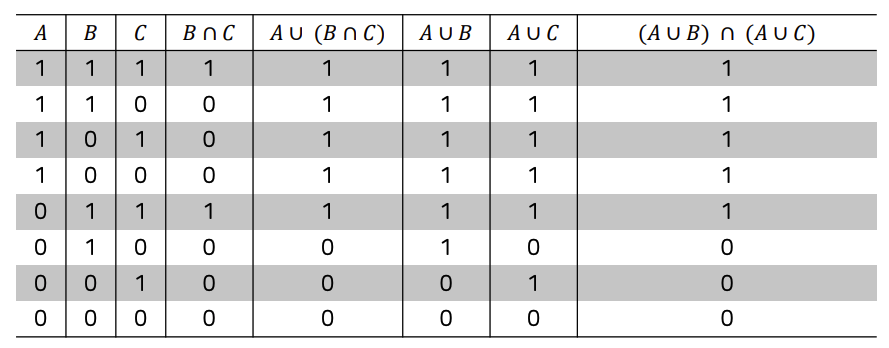
# 구성원 표를 이용한 증명

예제 풀이
합집합과 교집합의 일반화
- 여러 집합들의 합집합은 여러 집합들 중 적어도 하나의 집합에 나타나는 원소들을 포함한 집합이다.
컴퓨터에서의 집합 표현
- 컴퓨터에서의 집합 표현
- 우선 전체집합 U가 유한집합이라고 가정하면, 다음과 같이 비트열로 표현할 수 있다.
- U의 원소들을 a1, a2, ..., an과 같이 임의의 순서로 나열한다.
- U의 부분집합 A를 길이 n인 비트열로 표현한다.
- 비트열의 i번째 비트는 ai가 A의 원소일 경우 1로 표현하고, 원소가 아닐 경우 0으로 표현한다.

중복집합
- 원소가 한 번이상 나타나는 원소들의 순서 없는 모임이다.

'CS 대학강의' 카테고리의 다른 글
| [CS 1-2 | 시스템 프로그래밍 기초] 함수, 메모리에서의 변수&함수 7주차 (0) | 2022.09.27 |
|---|---|
| [CS 1-2 | 이산수학] 함수 7주차 (0) | 2022.09.27 |
| [CS 1-2 | 아카데믹 글쓰기] 고정관념, 여러 관점에서의 글쓰는 방법 3주차 (0) | 2022.09.26 |
| [CS 1-2 | 시스템 프로그래밍 기초] 피연산자와 연산자 7주차 (0) | 2022.09.23 |
| 프로그램 설계 방법론 - #05 [필드변수와 지역변수] (0) | 2022.09.23 |
