해당 포스팅은 강의시간에 진행했었던 개념을 잘 요약해서 설명하는 사진을
캡처해서 정리한다.
그렇기에, 시간이 남는다면..? 캡처한 자료를 토대로 블로그를 완성시킬 것이다 ㅎㅎ..
행렬의 연산인
덧셈, 뺼셈, 곱셈에 대해서 개념을 다시 학습해봐야겠다 ㅎㅎ...
문제를 풀려면 반드시 필요함 ㅎㅎ..
# 행렬의 기본 연산을 이용해서 원하는 행렬을 구성하는 법

# 행렬의 행렬식을 계산하는 사루스의 공식

# 행렬식의 성질 - 다음은 행렬식의 표준으로 활용된다.

# 행렬 - 전치행렬
# 행렬의 곱 - 행렬식의 곱

# 행렬의 어떤 행(또는 열)의 각 원소에 같은 k를 곱하여 얻은 행렬식과
처음 행렬식에 k를 곱한 것과 같다.

모든 행렬식의 성질은
사루스의 공식을 토대로 계산된 행렬식을 토대로 논증이 완료된
"행렬식의 정리"이다.
그렇기에, 이를 외울필요 없이 그 자리에서 사루스 공식을 사용해
해당 성질이 만족함을 깨달을 수 있다 ~~ㅎㅎ
# 기본행 연산을 이용해 행렬식 계산은
행렬식 성질을 토대로 작용하기에,
아래의 행렬식 성질만을 숙지해도 괜찮을 듯~!

# 기존 행렬을 대각 행렬로 재구성하고,
이에 대한 행렬식을 토대로 기존 행렬의 행렬식 추론하기
- 이때 대각행렬로 구성하면, 사루스 공식을 이용하면 결국 주대각선 곱이 행렬식 값이 된다~~
(아주 매직적으로 행렬식 암산으로 도출 ㄱㄴㄱㄴ)

# 소행렬과 소행렬식으로 3차 이상의 정사각행렬의 행렬식을 쉽게 구한다. - 소행렬을 조합해서 도출한다.

# 가우스 - 조단 방식의 역행렬 구하기로
역행렬을 쉽게 구할 수 있다~~ - 역행렬을 구하는 방법 중 좋은 방법의 하나이다.

# 가우스 - 조단 방식으로 역행렬 구하기 예제
다음과 같이 역행렬을 쉽게 구할 수 있다~~


# 역행렬을 이용한 선형연립방정식의 해 구하기~~


즉, 아래와 같이 선형방정식을 행렬로 바꿔주면서,
행렬에 대한 연산으로 선형방정식의 해를 "간접적으로" 구한다. - 컴퓨터는 행렬을 토대로 연산을 진행~!
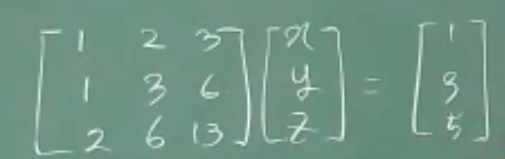
양변에 역행렬을 곱해줌으로써, 선형연립방정식의 해를 구한다.
이때, 양변에 무언가를 곱했으니 수학적으로 성립한다~~
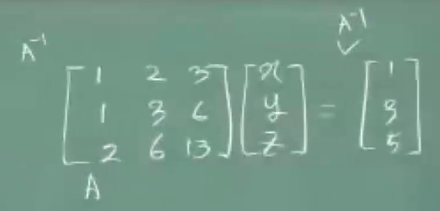
그럼, 다음과 같이 행렬 연산이 구성되고,
다음을 전개하면 구하고자 했던, "선형 연립방정식"의 해를 구할 수 있게 된다.
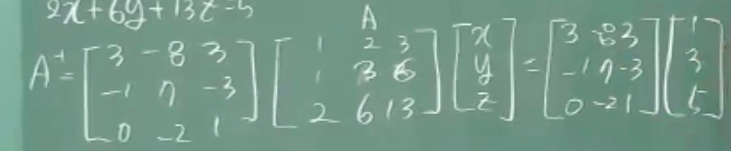
행렬에서 "행렬식"을 구하는 이유는
그 행렬과 관련된 행렬들을 구해보기 위해서이다.
그렇기에, 기존 행렬에 대한 행렬식으로
역행렬과 같은 기존 행렬과 연관된 행렬들을 구할 수 있다.
[기존행렬 X 기존 행렬의 역행렬 = 상등행렬이 되므로,
이를 활용해서 역행렬을 구할 수 있다~~ - 기존 행렬과 상등행렬은 사루스의 공식을 통해 추론이 가능하다 ㅎㅎ]
'CS 대학강의' 카테고리의 다른 글
| [CS 1-2 | 프로그램 설계 방법론] 배열 객체 & MVC 아키텍처 설계 실제 프로그램에 적용해보기 9주차 (2) | 2022.10.15 |
|---|---|
| [CS 1-2 | 오픈소스 SW 기초] 네트워크 통신 | 소켓 통신 5주차 (0) | 2022.10.13 |
| [CS 1-2 | 시스템 프로그래밍 기초] 디버깅과 소프트웨어 설계 10주차 (0) | 2022.10.11 |
| [CS 1-2 | 이산수학] 알고리즘 9주차 (0) | 2022.10.11 |
| 프로그램 설계 방법론 - 트러블 슈팅 [주사위 게임 과제] (0) | 2022.10.08 |
