수열
수를(구성요서) 순서에 맞춰 배열한 형태
규칙에 따라 수열의 특징을 지닐 수도 있다.
- 등비 수열
각항들의 비율이 같은 수열
- 등차 수열
각항들의 차이가 같은 수열
집합표현과 유사하지만, 혼동하지 않도록 유의해야 된다.
{an}
"수열은 n번째 나타나는 항의 식으로 표현할 수 있으며, 이 식을 '명백한공식'이라고도 함
앞서 나온 항들 간의 재귀적 규칙성을 이용해 다음에 올 항을 구할 수 있으며,
이런 관계를 '점화 관계'라 부른다."
수열의 점화 관계
- 점화 관계는 앞서 나온 항들 간의 재귀적 규칙성을 이용해 다음에 올 항들을 나타내는 것

예시
- 피보나치 수열
점화 관계의 해
- 초기 조건이 수반된 점화 관계를 푸시오 라는 말의 의미

주어진 수열로 점화 관계가 성립하는 지를 판단하여 해를 찾는다.
그리고, 점화 관계의 해는 고유가 아닌, 여러 개 존재할 수 있다.
점화 관계 해 찾는 법 - 반복법
반복법은 점화 관계를 반복적으로 사용하여 해를 찾는 방법
수를 하나씩 대입해보면서,
등차 수열임을 찾음.

특수한 정수수열
- - 앞의 몇 개 항만으로 수열의 일반적인 형태를 나타내는 공식이나 규칙을 찾을 때는 패턴을 찾아야 한다.
- 아래 규칙으로 쉽게 패턴을 찾음!
- 같은 값이 계속 나타나는 가?
- 앞의 항에 일정한 값을 더하거나 수열 내에서 위치에 관련되는 어떤 값을 더하면 다음 항을 얻을 수 있나?
- 앞의 항에 일정한 값을 곱하면 다음 항을 얻을 수 있는가?
- 앞의 항들을 어떠한 일정한 방식으로 조합하면 다음 항을 얻을 수 있는가?
- 항들이 일정한 규칙성을 갖고 순환되는가?
- 아래 규칙으로 쉽게 패턴을 찾음!
결국, 수열의 점화 관계는 "추론"을 통해 구할 수 있고,
여러 번의 점화 관계 도출 경험으로 자신만의 점화관계 추론 규칙을 세우게 된다.
많은 점화 관계 추론경험으로, 쉽게 점화관계를 도출해낸다.
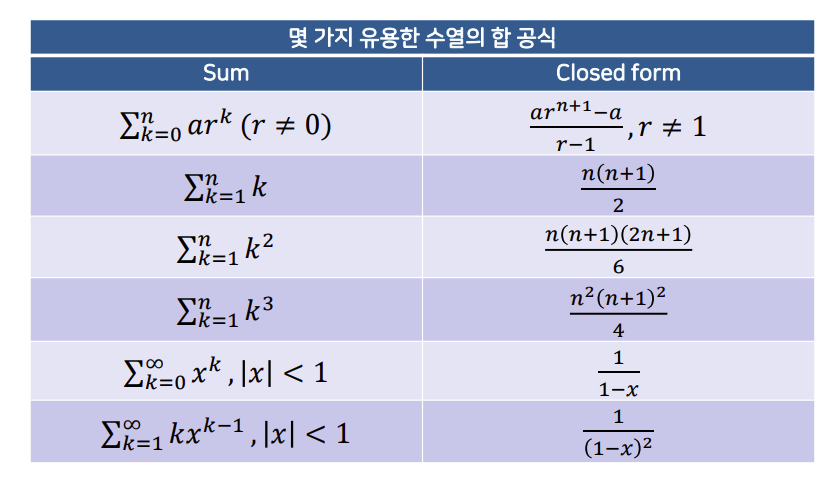
수열의 합 공식
아래는 수열의 합 공식이다.
k에 대한 합과
k^2에 대한 합 공식이 자주 쓰인다고, 교수님께서 언급하셨다.
행렬(Matrix)
행렬은 수를 사각형(2차원)으로 배열한 것이다. m개의 행(row)과 n개의 열(column)을 갖는 행렬을 m x n 행렬이라 부른다.
여러 개의 행렬을 행렬들이라고 한다.
- 행렬을 표현할 때, 행렬의 이름은 굵은 대문자를 사용한다.

# 행렬의 형태

행렬의 연산 - 덧셈
같은 크기의 두 행렬의 합은 해당 위치의 원소를 합해서 구할 수 있다.
두 행렬의 합은 두 행렬이 같은 수의 행과 같은 수의 열을 가질 때만 가능하다.
# 행렬의 연산 - 뺼셈 도 덧셈과 같은 원리를 지니지만, 행렬에 '-'를 곱해 행렬 덧셈연산으로 행렬 뺼셈 연산을 수행한다.
# 행렬의 연산 예시
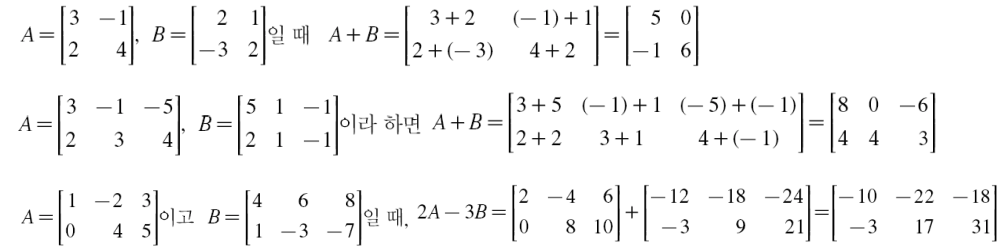
행렬의 연산 - 곱셈
행렬 곱을 수행하기 위해선, 다음과 같이 내측에 있는 값이 동일해야지만
행렬 곱을 수행할 수 있다.
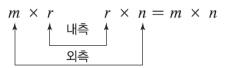

행렬의 곱은 ㄱ자 형태로 A의 한 행의 모든 원소와 B의 한 열의 모든 원소를 순차대로 곱해서 AB 곱한 행렬을 만든다.
행렬의 곱셈 - 특징


항등행렬


전치행렬과 대칭 행렬


해당 개념은 교수님께서 강조를 하지 않았음.
0-1 행렬 (Zero-one matrix)


# 0-1 행렬 예제

0-1 행렬의 부울 곱
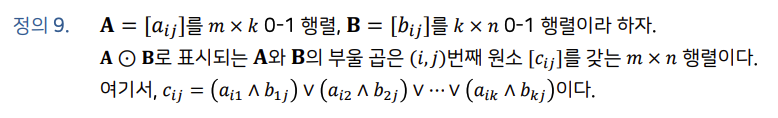
- 부울 곱은 일반적인 행렬의 곱셈과 유사하지만 덧셈은 V로 대체되고, 곱셈은 ∧로 대치된다.
# 행렬의 부울 곱 예제

0-1 행렬의 부울 거듭제곱

# 0-1 행렬의 부울 거듭제곱 예제

해당 개념은 교수님께서 강조를 하지 않았음.
'CS 대학강의' 카테고리의 다른 글
| [CS 1-2 | 대학생을 위한 실용금융] 저축과 세금 6주차 (0) | 2022.10.05 |
|---|---|
| [CS 1-2 | 시스템 프로그래밍 기초] 조건문과 반복문 9주차 (2) | 2022.10.04 |
| [CS 1-2 | 아카데믹 글쓰기] 글쓰기 꿀팁 4주차 (0) | 2022.10.03 |
| [CS 1-2 | 시스템 프로그래밍 기초] 함수 실습 8주차 (0) | 2022.09.30 |
| 프로그램 설계 방법론 - #07 [Java Aplication 구현 - 지갑 Aplication 확장] (0) | 2022.09.30 |
